Convergence of "Bent" Algorithm

This page contains a sketch of a proof for worst-case convergence of the "Bent" algorithm. Proofs for the best-case convergence (that of inverse quadratic interpolation) are readily available in the literature, so will not be reproduced here.

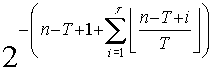
The symbols used in the proof are as follows:

The interactions of these parameters (given a function with such a large third derivative that inverse quadratic interpolation always fails to shrink the interval appreciably) is as shown in Table 1.

 
 
Iter # (n)
2-(a -t +1)  <=r -a < 2-(a -t )
r >= 2
t = 1
t = 2
. . .
t = a -2
t = a -1
t = a 
r <= 1
0
1
1
1
  
1
1
1
1
1
1
1
1
  
1
1
1
1
2
1
1
1
  
1
1
1
1
. . .
1
1
1
  
1
1
1
1
T-2
a -1
1
1
1
  
1
1
1
1
T-1
a 
1
1
1
  
1
1
1
1
T
a +1
2-1
2-1
2-1
  
2-1
2-1
2-1
1
T+1
a +2
2-2
2-2
2-2
  
2-2
2-2
2-1
1
T+2
a +3
2-3
2-3
2-3
  
2-3
2-2
2-1
1
T+3
a +4
2-4
2-4
2-4
  
2-3
2-2
2-1
1
. . .
                
2T-4
2a -2
2-(a -2)
2-(a -2)
2-(a -2)
  
2-3
2-2
2-1
1
2T-3
2a -1
2-(a -1)
2-(a -1)
2-(a -1)
  
2-3
2-2
2-1
1
2T-1
2a 
2-a 
2-a 
2-(a -1)
  
2-3
2-2
2-1
1
2T
2a +1
2-(a +1)
2-a 
2-(a -1)
  
2-3
2-2
2-1
1
2T+1
2a +2
2-(a +2)
2-(a +1)
2a 
  
2-4
2-3
2-2
1
2T+2
2a +3
2-(a +3)
2-(a +2)
2-(a +1)
  
2-5
2-4
2-2
1
2T+3
2a +4
2-(a +4)
2-(a +3)
2-(a +2)
  
2-6
2-4
2-2
1
2T+4
2a +5
2-(a +5)
2-(a +4)
2-(a +3)
  
2-6
2-4
2-2
1
. . .
                
3T-5
3a -2
2-(2a -2)
2-(2a -3)
2-(2a -4)
  
2-6
2-4
2-2
1
3T-4
3a -1
2-(2a -1)
2-(2a -2)
2-(2a -3)
  
2-6
2-4
2-2
1
3T-3
3a 
2-2a 
2-(2a -1)
2-(2a -2)
  
2-6
2-4
2-2
1
3T-2
3a +1
2-(2a +1)
2-2a 
2-(2a -2)
  
2-6
2-4
2-2
1
3T-1
3a +2
2-(2a +2)
2-2a 
2-(2a -2)
  
2-6
2-4
2-2
1
3T
3a +3
2-(2a +3)
2-(2a +1)
2-(2a -1)
  
2-7
2-5
2-3
1
3T+1
3a +4
2-(2a +4)
2-(2a +2)
2-2a 
  
2-8
2-6
2-3
1
3T+2
3a +5
2-(2a +5)
2-(2a +3)
2-(2a +1)
  
2-9
2-6
2-3
1
3T+3
3a +6
2-(2a +6)
2-(2a +4)
2-(2a +2)
  
2-9
2-6
2-3
1
Table 1: Diagram of Worst-Case Convergence Rates as a Function of r

The red entries in the table indicate steps where bisection was performed. Setting t to zero (or, equivalently, r to at least 2) represents an extreme case where bisection is always used once the history table has been fully populated. Similarly, setting r =1 or less represents an extreme case where bisection will never be used (unless forced by nonmonotonicities in the objective function).

The table is constructed using the basic rule of the Bent algorithm: if the interval of convergence has not shrunk by at least a factor of r^a over the past a iterations, then take a bisection step, else take a inverse-quadratic-interpolation step.

The pattern in Table 1, where each value of r allows quadratic interpolation to be used at least t times during each cycle of length a +1=T through the history table, can be cast into equation form as a lower bound on convergence. After n iterations, where n   T-1, the initial interval containing the root will be reduced by at least the ratio given by Equation 1:
 
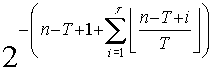Equation 1
 

 
Having T and r simultaneously large seems to be a good compromise between the need to use bisection when higher-order methods fail to converge rapidly and the need to allow for the less-deterministic convergence of higher-order methods. Setting T to 8 and r to 1.9 works well for most functions. The reason for this is that the 8 iterations history-fill interval allows inverse quadratic interpolation to reach the region of quadratic convergence in most cases, while functions that must use bisection require so many evaluations that the additional 8 to fill the history array is often of little concern, assuming that most functions of interest respond well to higher-order methods.

Given a predetermined value of a and t , use Equation 2 to select a value for r .
 
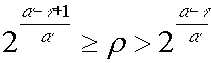Equation 2
 

 
The worst-case convergence is at best that of bisection. The best-case convergence is obtained for functions of the form shown in Equation 3.
 
Equation 3
 
 
Inverse quadratic interpolation solves this family of functions exactly in four evaluations, given sufficiently accurate machine arithmetic.